Regular prime
In number theory, a regular prime is a prime number p > 2 that does not divide the class number of the p-th cyclotomic field.
The first few regular primes are:
- 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, ... (sequence A007703 in OEIS)
Are there infinitely many regular primes, and if so is their relative density 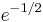 ? ? |
Contents |
Kummer's criterion
Ernst Kummer (Kummer 1850) showed that an equivalent criterion for regularity is that p does not divide the numerator of any of the Bernoulli numbers Bk for k = 2, 4, 6, …, p − 3.
Properties
It has been conjectured that there are infinitely many regular primes. More precisely Siegel conjectured (1964) that e−1/2, or about 60.65%, of all prime numbers are regular, in the asymptotic sense of natural density. Neither conjecture has been proven as of 2010[update].
Irregular primes
An odd prime that is not regular is an irregular prime. The first few irregular primes are:
- 37, 59, 67, 101, 103, 131, 149, ... (sequence A000928 in OEIS)
K. L. Jensen has shown in 1915 that there are infinitely many irregular primes.
Metsänkylä proved[1] that for any integer T > 6, there are infinitely many irregular primes not of the form mT + 1 or mT − 1.
Irregular pairs
If p is an irregular prime and p divides the numerator of the Bernoulli number B2k for 0 < 2k < p − 1, then (p, 2k) is called an irregular pair. The first few irregular pairs are:
- (691, 12), (3617, 16), (43867, 18), (283, 20), (617, 20), (131, 22), (593, 22), (103, 24), ... (sequence A189683 in OEIS).
For a given prime p, the number of such pairs is called the index of irregularity of p. Hence, a prime is regular if and only if its index of irregularity is zero. Similarly, a prime is irregular if and only if its index of irregularity is positive.
It was discovered that (p, p − 3) is in fact an irregular pair for p = 16843. This is the first and only time this occurs for p < 30000.
History
In 1850, Kummer proved that Fermat's Last Theorem is true for a prime exponent p if p is regular. This raised attention in the irregular primes.[2] In 1852, Genocchi was able to prove that the first case of Fermat's Last Theorem is true for an exponent p, if (p, p − 3) is not an irregular pair. Kummer improved this further in 1857 by showing that for the first case of Fermat's Last Theorem it is sufficient to establish that either (p, p − 3) or (p, p − 5) fails to be an irregular pair.
Kummer found the irregular primes less than 165. In 1963, Lehmer reported results up to 10000 and Selfridge and Pollack announced in 1964 to have completed the table of irregular primes up to 25000. Although the two latter tables did not appear in print, Johnson found that (p, p − 3) is in fact an irregular pair for p = 16843 and that this is the first and only time this occurs for p < 30000.[3]
See also
References
- ^ Tauno Metsänkylä (1971). "Note on the distribution of irregular primes". Ann. Acad. Sci. Fenn. Ser. A I 492. MR0274403.
- ^ Gardiner, A. (1988), "Four Problems on Prime Power Divisibility", American Mathematical Monthly 95 (10): 926–931, doi:10.2307/2322386
- ^ Johnson, W. (1975), "Irregular Primes and Cyclotomic Invariants", Mathematics of Computation 29 (129): 113–120, http://www.ams.org/journals/mcom/1975-29-129/S0025-5718-1975-0376606-9/S0025-5718-1975-0376606-9.pdf Archived at WebCite
Further reading
- Kummer, E. E. (1850), "Allgemeiner Beweis des Fermat'schen Satzes, dass die Gleichung xλ + yλ = zλ durch ganze Zahlen unlösbar ist, für alle diejenigen Potenz-Exponenten λ, welche ungerade Primzahlen sind und in den Zählern der ersten (λ-3)/2 Bernoulli'schen Zahlen als Factoren nicht vorkommen", J. Reine Angew. Math. 40: 131–138, http://www.digizeitschriften.de/resolveppn/GDZPPN002146738
- Carl Ludwig Siegel (1964). "Zu zwei Bemerkungen Kummers". Nachr. Akad. d. Wiss. Goettingen, Math. Phys. K1. II: 51–62.
- Iwasawa, K.; Sims, C. C. (1966), "Computation of invariants in the theory of cyclotomic fields", Journal of the Mathematical Society of Japan 18 (1): 86–96, doi:10.2969/jmsj/01810086, http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdf_1&handle=euclid.jmsj/1260541355 Archived at WebCite
- Wagstaff, Jr., S. S. (1978), "The Irregular Primes to 125000", Mathematics of Computation 32 (142): 583–591, http://www.ams.org/journals/mcom/1978-32-142/S0025-5718-1978-0491465-4/S0025-5718-1978-0491465-4.pdf Archived at WebCite
- Granville, A.; Monagan, M. B. (1988), "The First Case of Fermat's Last Theorem is True for All Prime Exponents up to 714,591,416,091,389", Transactions of the American Mathematical Society 306 (1): 329–359, MR0002994788, http://www.ams.org/journals/tran/1988-306-01/S0002-9947-1988-0927694-5/S0002-9947-1988-0927694-5.pdfarchived at WebCite
- Gardiner, A. (1988), "Four Problems on Prime Power Divisibility", American Mathematical Monthly 95 (10): 926–931, doi:10.2307/2322386
- Ernvall, R.; Metsänkylä, T. (1991), "Cyclotomic Invariants for Primes Between 125000 and 150000", Mathematics of Computation 56 (194): 851–858, http://www.ams.org/journals/mcom/1991-56-194/S0025-5718-1991-1068819-7/S0025-5718-1991-1068819-7.pdf Archived at WebCite
- Ernvall, R.; Metsänkylä, T. (1992), "Cyclotomic Invariants for Primes to One Million", Mathematics of Computation 59 (199): 249–250, http://www.ams.org/journals/mcom/1992-59-199/S0025-5718-1992-1134727-7/S0025-5718-1992-1134727-7.pdf
- Buhler, J. P.; Crandall, R. E.; Sompolski, R. W. (1992), "Irregular Primes to One Million", Mathematics of Computation 59 (200): 717–722, http://www.ams.org/journals/mcom/1992-59-200/S0025-5718-1992-1134717-4/S0025-5718-1992-1134717-4.pdf Archived at WebCite
- Boyd, D. W. (1994). "A p-adic Study of the Partial Sums of the Harmonic Series". Experimental Mathematics (A K Peters, Ltd.) 3 (4): 287–302. doi:10.1.1.56.7026. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.56.7026&rep=rep1&type=pdf.archived at WebCite
- Shokrollahi, M. A. (1996), "Computation of Irregular Primes up to Eight Million (Preliminary Report)", ICSI Technical Report TR-96-002, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.38.4040&rep=rep1&type=pdfArchived at WebCite
- Buhler, J.; Crandall, R.; Ernvall, R.; Metsänkylä, T.; Shokrollahi, M.A. (2001), "Irregular Primes and Cyclotomic Invariants to 12 Million", Journal of Symbolic Computation 31 (1-2): 89–96, doi:10.1006/jsco.1999.1011
- Richard K. Guy (2004). "Section D2. The Fermat Problem". Unsolved Problems in Number Theory (3rd ed.). Springer Verlag. ISBN 0-387-20860-7.
- Villegas, F. R. (2007). Experimental Number Theory. New York: Oxford University Press. pp. 166–167. ISBN 9780198528227. http://books.google.com/books?id=xXNFmoEaD9QC&pg=PA166.
External links
- Chris Caldwell, The Prime Glossary: regular prime at The Prime Pages.
- Keith Conrad, Fermat's last theorem for regular primes.